„Wohl steht das Haus gezimmert und gefügt, doch ach – es wankt der Grund, auf den wir bauten.“ (Friedrich von Schiller)
Seit dem Aufkommen von Value-at-Risk-Maßen bei Banken zur Messung diverser Marktrisiken haben sich diese auch bei Versicherungen zu einem gewissen Marktstandard entwickelt. Die „Kernzahl“ im Kontext der Solvency-II-Richtlinie ist gerade durch den Value-at-Risk des Gesamt-Portfolios (Anlage- und Verpflichtungsseite) zum Niveau 99,5% gegeben, das p-Quantil qp zur Wahrscheinlichkeit p=0,05% wird dabei fälschlicherweise auch als „200-Jahres-Ereignis“ bezeichnet.
Der klassische Value-at-Risk unterschätzt das Risiko bei Fat Tails
Der am häufigsten geäußerte Kritikpunkt bezieht sich darauf, dass der klassische Value-at-Risk bei sogenannten „Fat Tails“ das Risiko unterschätzt, d.h. seltene, extrem adverse Ereignisse (von Nassim Nicholas Taleb populärwissenschaftlich als „Black Swans“ tituliert) nicht genügend berücksichtigt. Wir wollen auf einen weiteren Hemmschuh hinweisen: Die Schätzung von p-Quantilen für sehr kleine oder sehr große Wahrscheinlichkeiten ist – ganz im Gegensatz z.B. zum Median mit p=50% – recht ungenau. Es ist gerade nicht ausreichend, beispielsweise 1.000 Simulationen durchzuführen, absteigend zu sortieren und dann einfach das Ergebnis Nr. 995 anzuführen. Das klassische Schätzverfahren liefert grundsätzlich ein Konfidenz-Intervall zu einer vorgegebenen Irrtumswahrscheinlichkeit α, d.h. mit Sicherheit 1-α liegt das zu schätzende p-Quantil im angegebenen Intervall. Selbstverständlich möchte man α klein wählen. Sind die n Simulationen folgendermaßen sortiert:
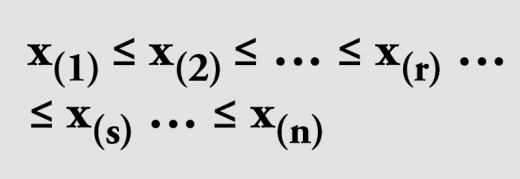
dann berechnet man zunächst mit dem 1-α/2-Quantil u1-α/2 der Standardnormalverteilung die Zahlen:

Diese rundet man schließlich auf die nächstgrößeren Zahlen r und s auf und erhält als Konfidenzintervall zum Niveau 1-α für qp:
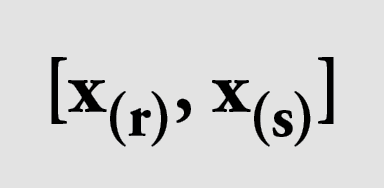
Wir haben diese Berechnung für verschiedene n und α durchgeführt. Hierbei gilt es, zwischen hoher Schätzgenauigkeit auf der einen und der Anzahl teurer und zeitaufwendiger Simulationen auf der anderen Seite abzuwägen. Man wählt α also möglichst klein, schließlich möchte man das Risiko genau kennen, darf aber auch nicht „übervorsichtig“ sein und zu viel Solvency Capital Requirement zurückstellen. Tabelle 1 zeigt eine Übersicht zunächst mit einer relativ großen Irrtumswahrscheinlichkeit von 20%, also 1-α=80%. Wir stellen die Anzahl n der durchgeführten Simulationen, die wie oben angegebenen Indices r und s des Konfidenzintervalls sowie dessen Breite (absolut und relativ zu n) gegenüber. Auffällig- und Unstimmigkeiten sind rosa unterlegt. Es fällt auf, dass bei niedrigen Anzahlen, d.h. 100 und 500, die Werte für s im ersten Fall (101 > 100) sinnlos und im zweiten Fall (500 = n) redundant sind.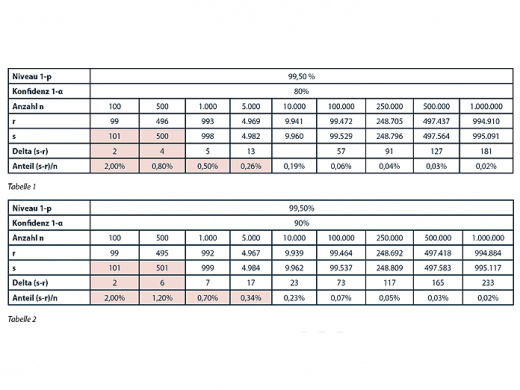
Auf Simulationen mit weniger als 5.000 Runs kann man getrost verzichten
Selbst bei 1.000 Simulationen ist der Konfidenzbereich in der gleichen Größenordnung wie p. Es zeigt sich also, dass man auf Simulationen mit weniger als 5.000 Runs getrost verzichten kann. Wie sieht es jedoch bei höherem Konfidenz-Niveau aus? Tabelle 2 liefert „doppelt so sichere“ Werte wie Tabelle 1, d.h. die Irrtumswahrscheinlichkeit α ist nur noch 10%. Hier wird es beim – in der Statistik durchaus üblichen – Konfidenz-Niveau von 90% erst ab 10.000 Runs interessant. Zu guter Letzt zeigen die Tabellen 3 und 4 die Auswertungen zu Niveaus von 95% bzw. 99%. Es ist a priori klar, dass man für eine höhere Genauigkeit mehr Simulationen benötigt. In beiden Fällen sollte schon mindestens 100.000-mal simuliert werden, um überhaupt ein verlässliches Ergebnis zu erhalten.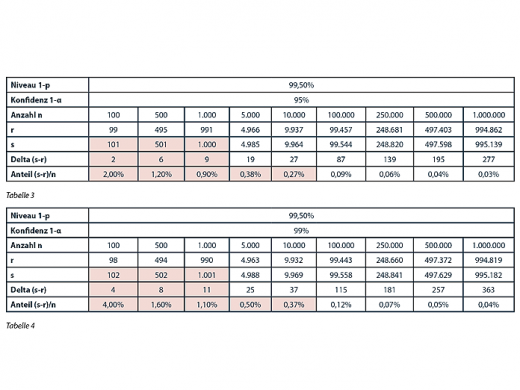
Wie bei allen (vereinfachenden) Modellbildungen ist jedoch Vorsicht geboten, in diesem Fall aber nicht nur beim Transfer Realität → Modell und zurück, sondern auch bei der mathematischen Umsetzung.







